等边梯形的周长公式是什么?
小学初接触平面图形,主要一些基本认识和计算周长和面积。包含点、线、三角形、四边形等。平面图形也是平面几何的基础,掌握好基本认识和基本公式,也是打好平面几何的学习基础。
周长:围成一个图形的所有边长的总和就是这个图形的周长。
面积:物体的表面或围成的平面图形的大小,叫作它们的面积。
1. 平面图形周长计算公式
(1)长方形的周长=(长+宽)×2
(2)正方形的周长=边长×4
(3)平行四边形周长=(长边+短边)×2
(4)三角形周长=三边之和
(5)圆的直径=半径×2
(6)圆的半径=直径÷2
(7)圆的周长=圆周率×直径=圆周率×半径×2
(8)梯形周长=上底+下底+腰长+腰长
扇形周长=半径×2+ 2×π×半径×
2. 平面图形的面积公式
(1)长方形的面积=长×宽
(2)正方形的面积=边长×边长
(3)平行四边形面积=底×高
(4)三角形的面积=底×高÷2
(5)平行四边形的面积=底×高
(6)梯形的面积=(上底+下底)×高÷2
(7)圆的面积=圆周率×半径×半径
扇形面积= 半径×半径×π×
1. 线和角
(1)端点
端点是指线段或射线的起点或终点。
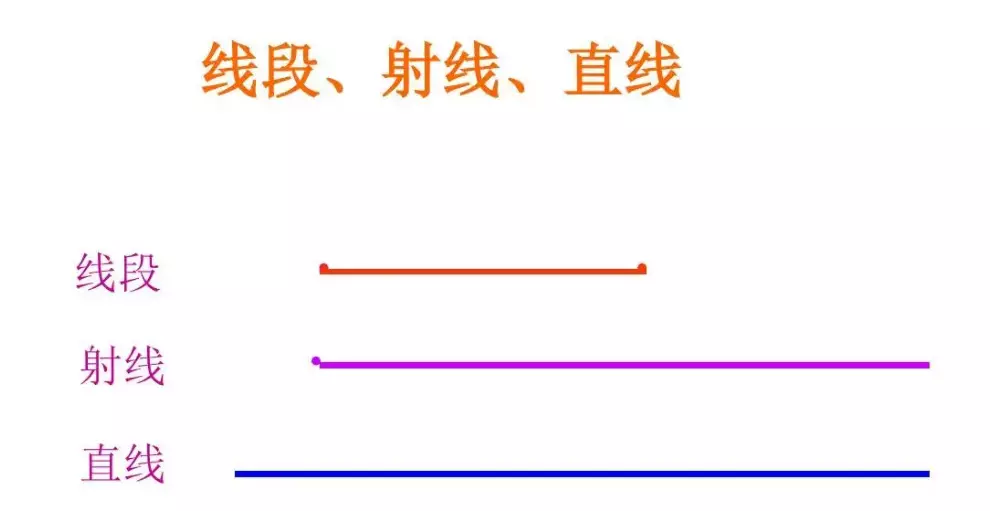
(2)线段
线段是指直线上两点间的有限部分(包括两个端点)。
(3)直线
直线是不弯曲的线,没有端点,可以向两端无限延长。过一点可以画无数条直线,过两点只能画一条直线。
(4)射线
射线指线段的一端无限延长,形成一条直的线,无法测量长度。比如:手电筒发出的光。
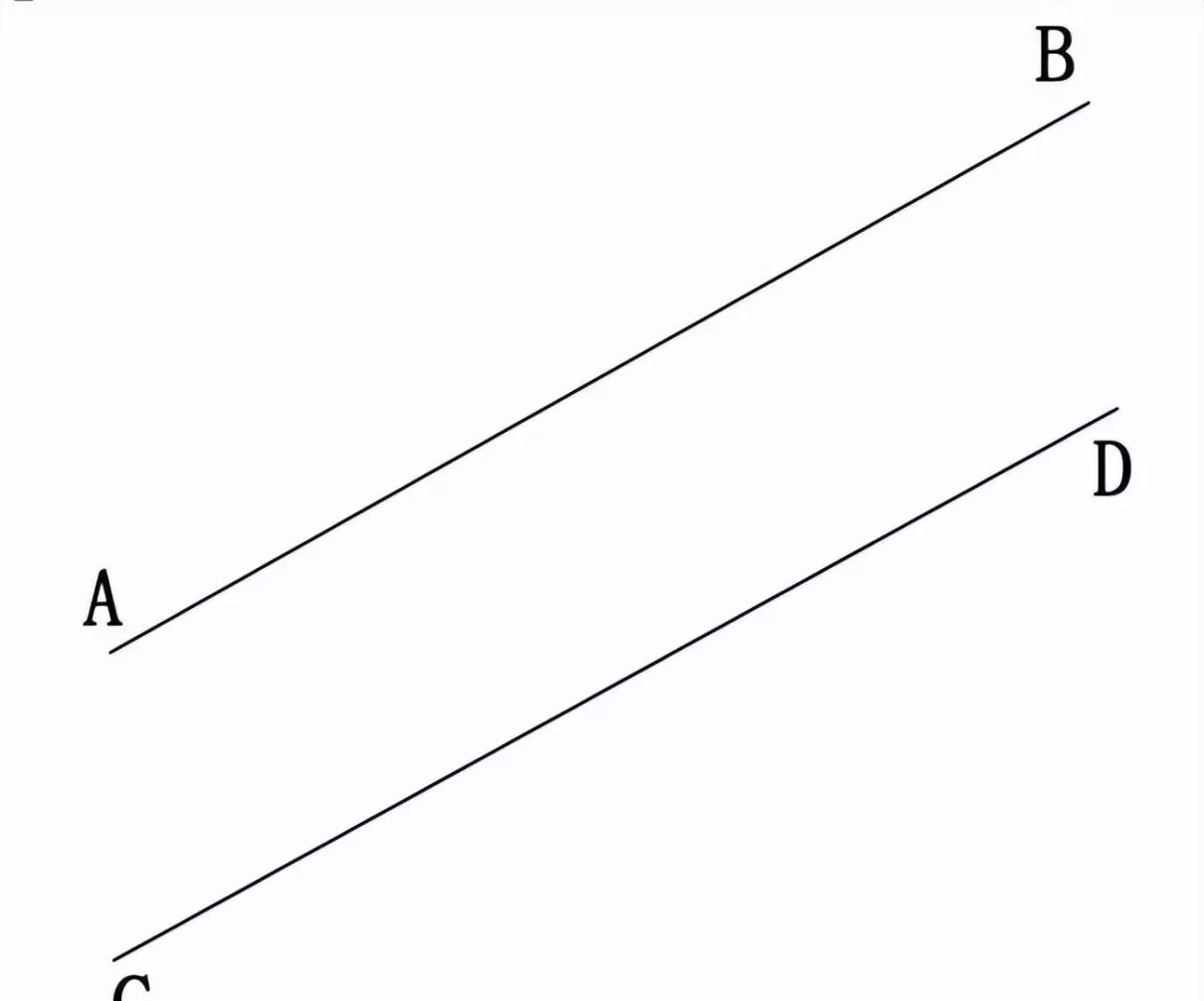
(5)平行线
在同一个平面内,两条不相交的线,就是平行线。
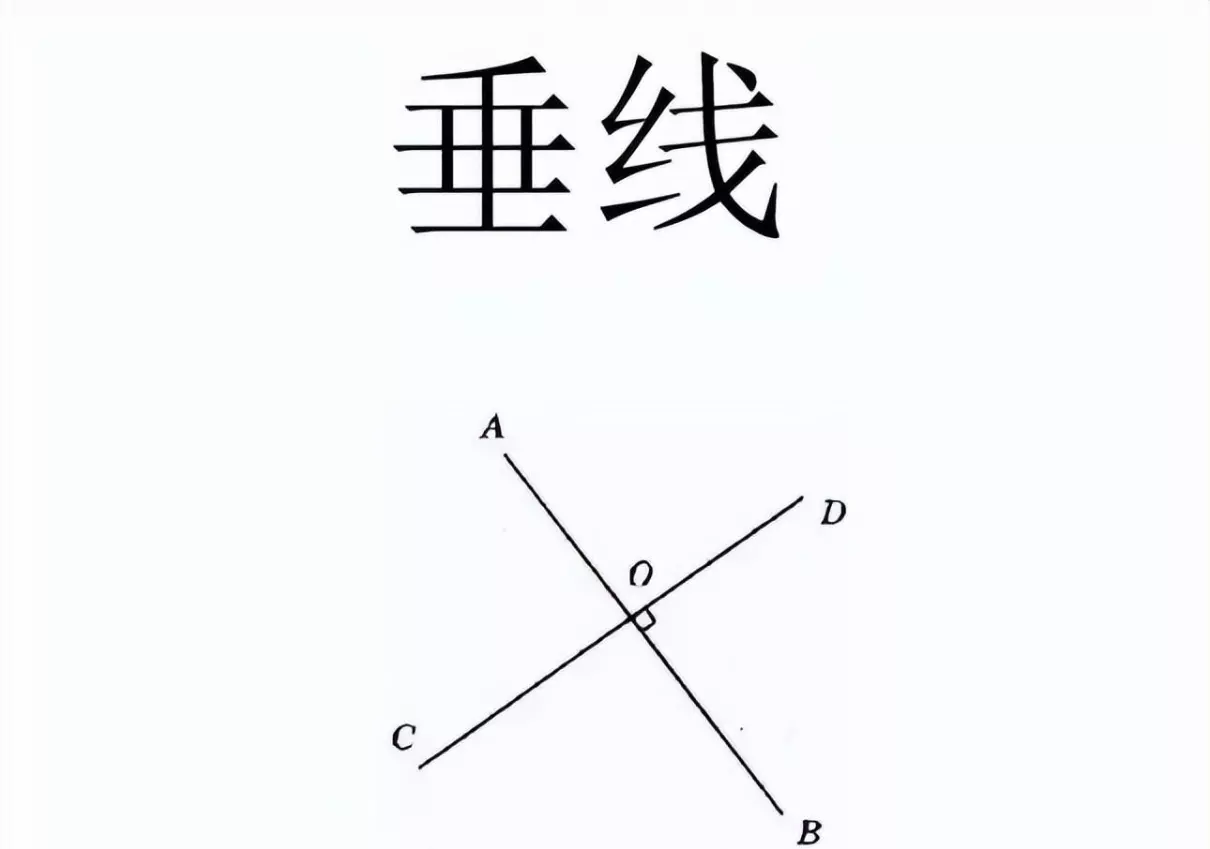
(6)垂线
两条直线相交形成直角(角度为90度),这两条直线互相垂直。其中一条直线是另一条直线的垂线。两条直线相交的点,叫作垂足。
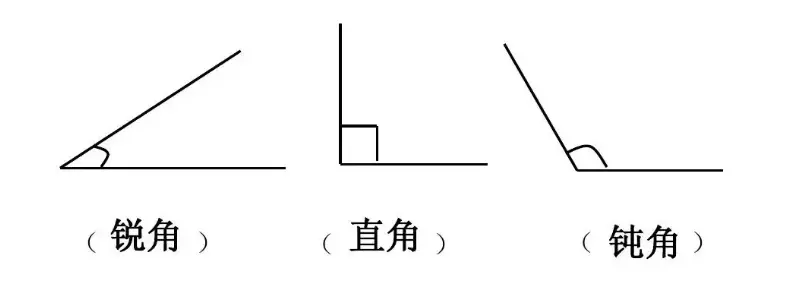
(7)角及分类
从同一点引出的两条射线所形成的图形是角。
小于90度的角叫锐角,等于90度的角为直角,大于90度的角为钝角。
2. 平面图形
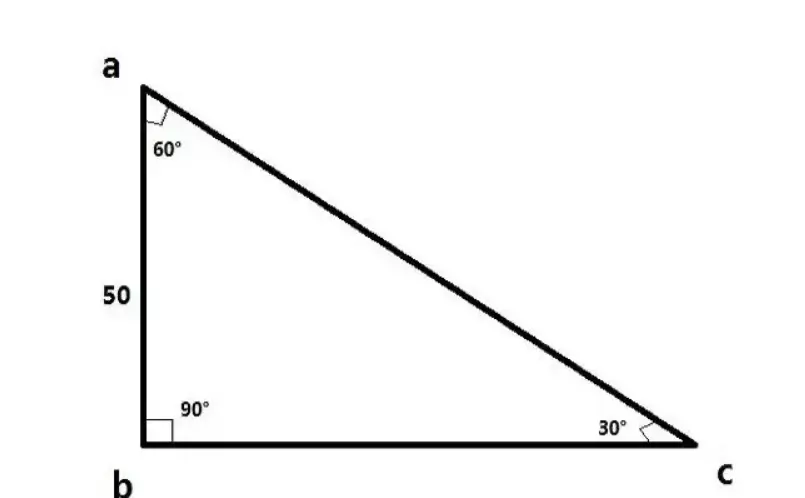
(1)三角形
由不在同一条直线上的三条线段首尾顺次相接,所组成的图形叫作三角形。三角形的三个内角之和是180度。
组成三角形的三条线段,叫作三角形的边。
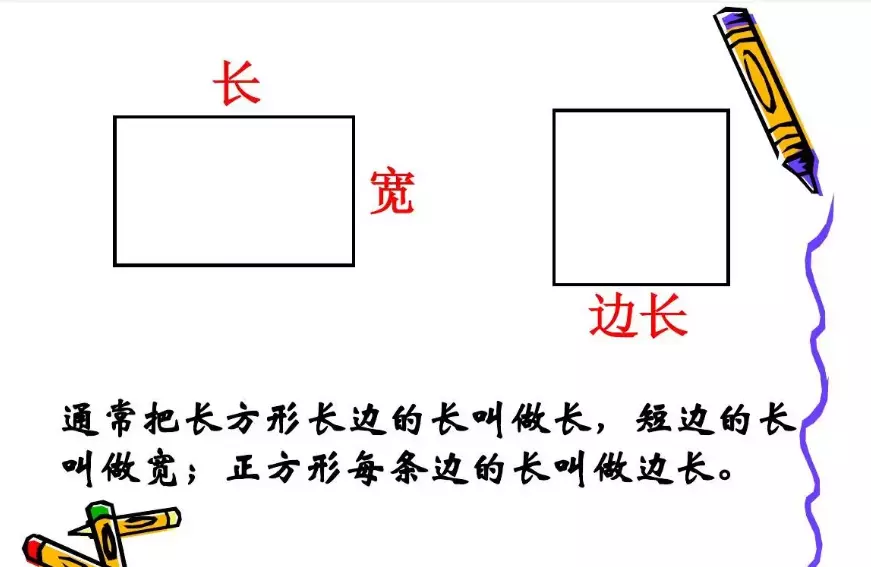
(2)长方形
四个角都是直角的平行四边形叫长方形。
(3)正方形
两条相邻的边相等并且有一个角是直角的四边形,叫正方形。
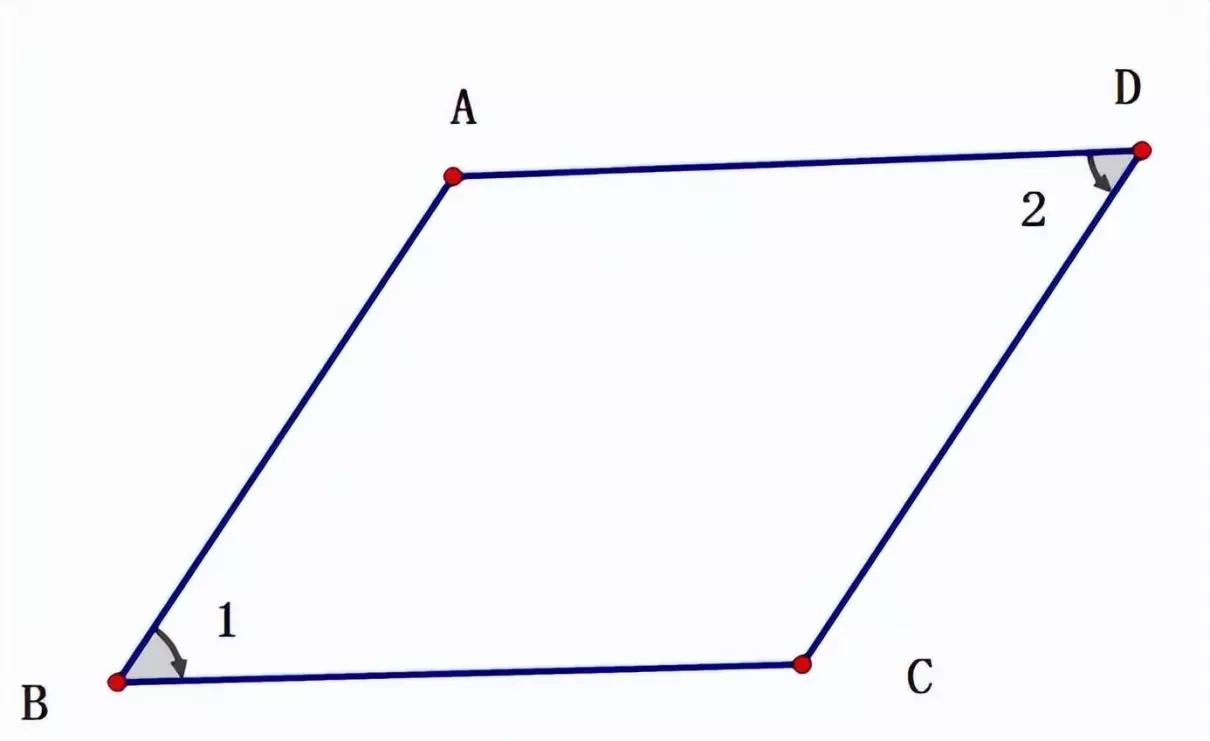
(4) 平行四边形
四边形两组相对的边,分别平行的四边形是平行四边形。长方形和正方形都是特殊的平行四边形。
平行四边形相对的边平行且相等,对角相等,相邻的两个角之和为180度。
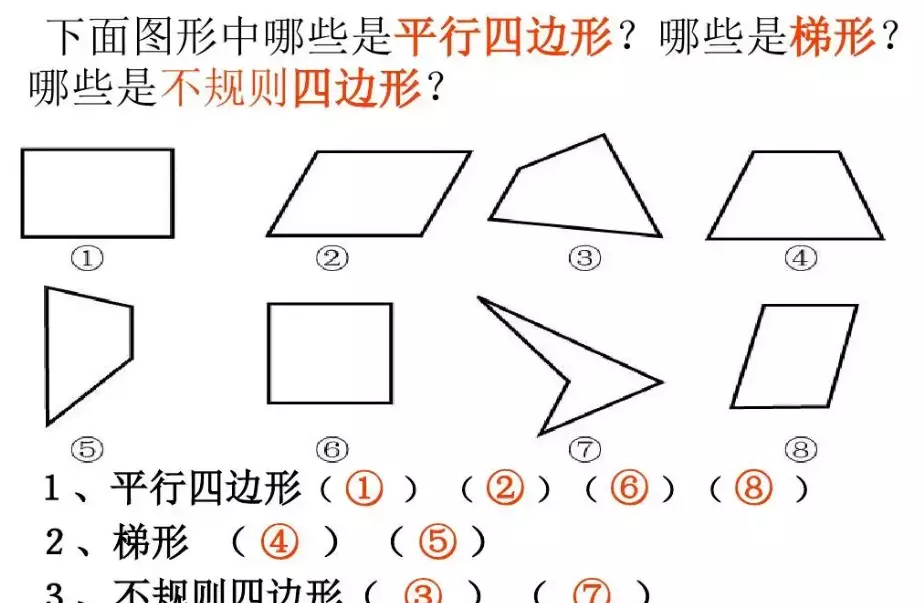
(5)梯形
一组边平行,一组边不平行的四边形是梯形。
3. 圆形
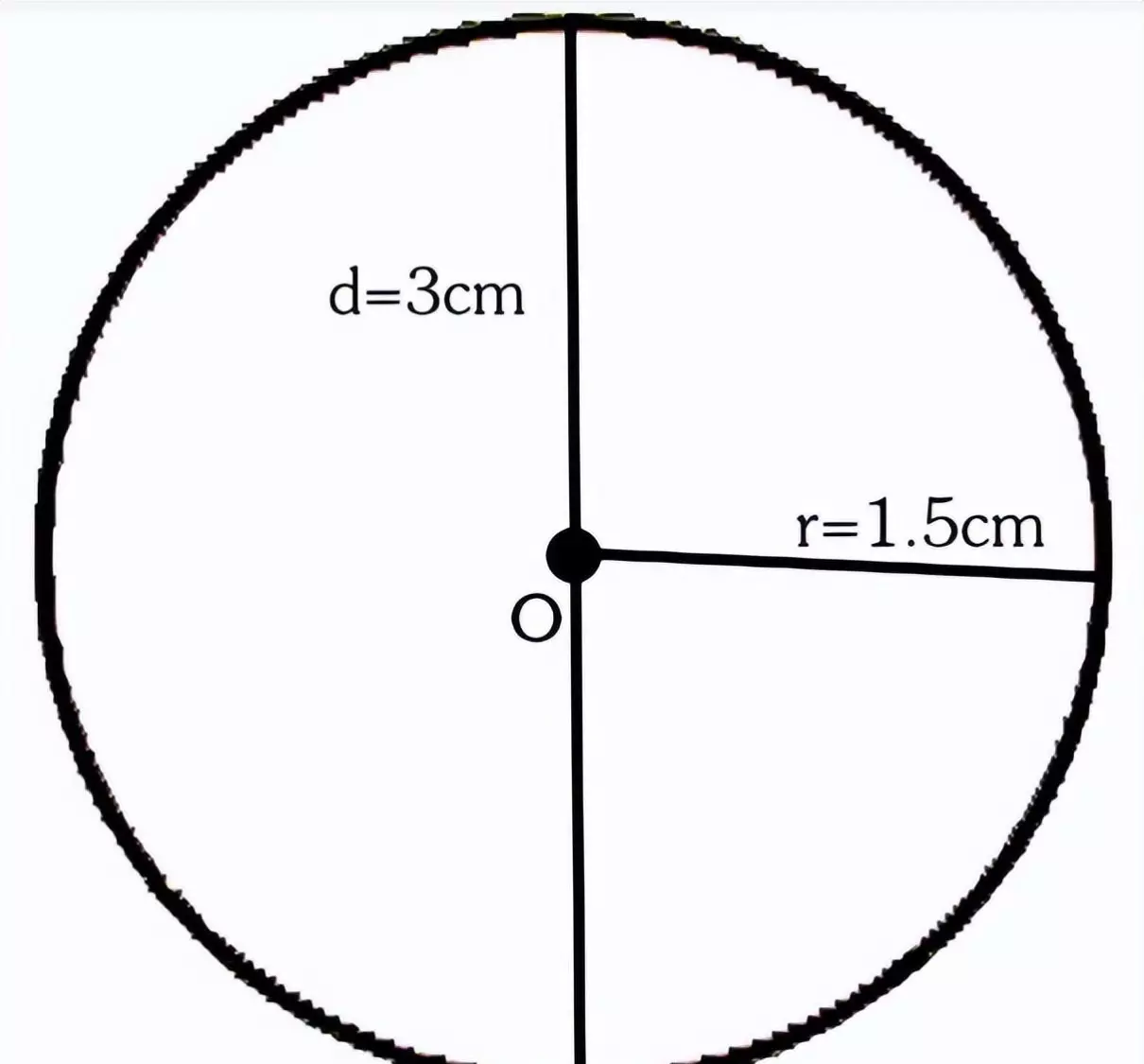
在一个平面内,围绕一个点并以一定长度为距离旋转一周,所形成的封闭曲线叫作圆。
圆的中心叫作圆心。圆心和圆线段上的点相连,则是圆的半径。通过圆心并且两端都在圆上的线段叫作直径。在同一个圆内,直径是半径的2倍。
4. 扇形
一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形。
扇形半径就是两条线段,扇形直径是两倍的线段。
相关文章
-
半球体表面积公式怎么算
半球体表面积,体积公式及计算器 半球是圆球体的一半。它是一个三维几何对象。计算半径、 弯曲的表面积、 半圆端面表面积、 总表面积、 体积和圆周的半球您必须具有这些条件的任何一项。半球表面积 =(4R2)/2+R2= 3 r2 公式:体积= r3 2016年9月11号修改...
2024-02-27 阅读 (143) -
一个等腰三角形的一条边长为14厘米,它的周长是多少
假设我们有一个等腰三角形,它的两条腰是相等的,我们称它们为$h$。底边是$b$。我们知道,一个三角形的周长就是它的三条边的长度之和。所以,这个等腰三角形的周长$P$就是两条腰的长度加上底边的长度,也就是$2h + b$。等腰三角形的周长计算方法是:将两条等长的腰加上底边的长度。假设等腰三角形的底边长度为$b$,腰的长度为$h$,那么周长$P$的计算公式为:
2024-08-11 阅读 (105) -
sinn次方的定积分公式0到pai/2
关于(sinx)^n 从0到pi/2的定积分有个公式叫Wallis公式,也叫华莱士公式。Wallis公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作用。Wallis(华里士)公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作
2024-08-12 阅读 (203) -
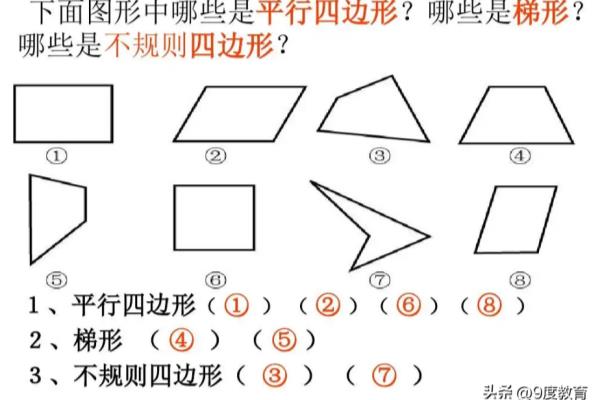
等边梯形的周长公式是什么?
小学初接触平面图形,主要一些基本认识和计算周长和面积。包含点、线、三角形、四边形等。平面图形也是平面几何的基础,掌握好基本认识和基本公式,也是打好平面几何的学习基础。周长:围成一个图形的所有边长的总和就是这个图形的周长。1. 平面图形周长计算公式 (2)正方形的周长=边长×4 四个角都是直角的平行四边形叫长方形。
2024-03-21 阅读 (121) -
cosc等于什么公式
cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB。余弦定理,欧氏平面几何学基本定理。余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广,勾股定理是余弦定理的特例。余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求三角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
2024-05-22 阅读 (113) -
麦克劳林公式需要x趋近于0吗
两种方法比较一下,明眼人都能看得出来,利用麦克劳林公式的方法要简便得多。不过运用麦克劳林展开式求极限有一个前提,那就是x必须是趋于0的。如果您觉得上面这种方法也挺简单的,那也可以坚持用这种方法的。不过下面利用麦克劳林公式求解的方法,肯定要简便得多的。解2:【利用麦克劳林公式的关键是熟记常用函数的麦克劳林展开式,其中】
2024-04-06 阅读 (105) -
澳洲幸运8破解公式方法
除此之外还有一点就是幸运8只是打出上限攻击的几率变高而已,如果运气不好刀刀打出最低下限也不是不可能的。而幸运9却可以保证每一刀都是最高伤害。换句话说如果运气不好的时候,幸运8和幸运1是一样的,伤害不稳定。而幸运9的伤害就稳定得多了。其实这种说法是比较极端的,于是我准备亲自做一下实验。那么就有玩家感到好奇了,幸运8与幸运9的差距只有一点,这能有多大的差距呢?可能很多玩家会认为差距不大。其实不然,幸运8与幸运9的差距是天差地别的。幸运8只有90%的几率打出最高伤害,而幸运9却可以每一刀都是最高伤害。
2024-03-09 阅读 (131)
热门资讯
-
关于(sinx)^n 从0到pi/2的定积分有个公式叫Wallis公式,也叫华莱士公式。Wallis公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作用。Wallis(华里士)公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作
2024-08-12 阅读 (203) -
半球体表面积,体积公式及计算器 半球是圆球体的一半。它是一个三维几何对象。计算半径、 弯曲的表面积、 半圆端面表面积、 总表面积、 体积和圆周的半球您必须具有这些条件的任何一项。半球表面积 =(4R2)/2+R2= 3 r2 公式:体积= r3 2016年9月11号修改...
2024-02-27 阅读 (143) -
 2024-03-09 阅读 (131)
2024-03-09 阅读 (131) -
 2024-03-21 阅读 (121)
2024-03-21 阅读 (121) -
cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB。余弦定理,欧氏平面几何学基本定理。余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广,勾股定理是余弦定理的特例。余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求三角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
2024-05-22 阅读 (113)
最新资讯
-
关于(sinx)^n 从0到pi/2的定积分有个公式叫Wallis公式,也叫华莱士公式。Wallis公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作用。Wallis(华里士)公式是关于圆周率的无穷乘积的公式,但Wallis公式中只有乘除运算,连开方都不需要,形式上十分简单。虽然Wallis公式对π的近似计算没有直接影响,但是在导出Stirling公式中起到了重要作
2024-08-12 阅读 (203) -
假设我们有一个等腰三角形,它的两条腰是相等的,我们称它们为$h$。底边是$b$。我们知道,一个三角形的周长就是它的三条边的长度之和。所以,这个等腰三角形的周长$P$就是两条腰的长度加上底边的长度,也就是$2h + b$。等腰三角形的周长计算方法是:将两条等长的腰加上底边的长度。假设等腰三角形的底边长度为$b$,腰的长度为$h$,那么周长$P$的计算公式为:
2024-08-11 阅读 (105) -
cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB。余弦定理,欧氏平面几何学基本定理。余弦定理是描述三角形中三边长度与一个角的余弦值关系的数学定理,是勾股定理在一般三角形情形下的推广,勾股定理是余弦定理的特例。余弦定理是揭示三角形边角关系的重要定理,直接运用它可解决一类已知三角形两边及夹角求第三边或者是已知三个边求三角的问题,若对余弦定理加以变形并适当移于其它知识,则使用起来更为方便、灵活。
2024-05-22 阅读 (113) -
两种方法比较一下,明眼人都能看得出来,利用麦克劳林公式的方法要简便得多。不过运用麦克劳林展开式求极限有一个前提,那就是x必须是趋于0的。如果您觉得上面这种方法也挺简单的,那也可以坚持用这种方法的。不过下面利用麦克劳林公式求解的方法,肯定要简便得多的。解2:【利用麦克劳林公式的关键是熟记常用函数的麦克劳林展开式,其中】
2024-04-06 阅读 (105) -
 2024-03-21 阅读 (121)
2024-03-21 阅读 (121)