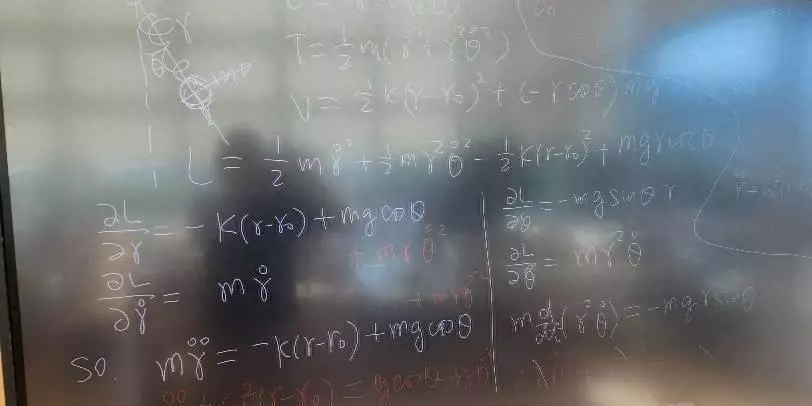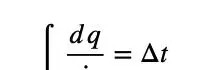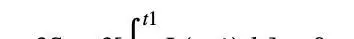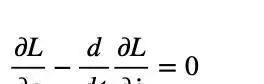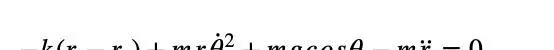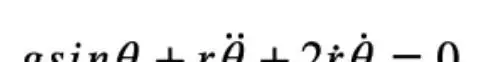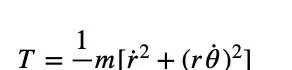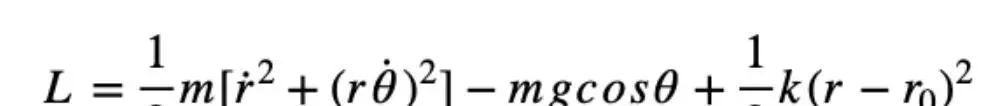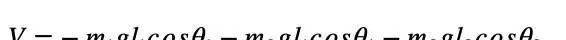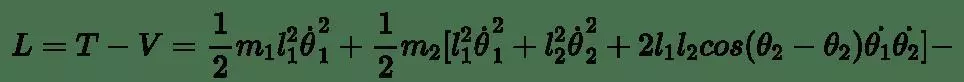怎么知道是双摆还是单摆

拉格朗日力学：弹簧摆和双摆的案例分析在物理学中，我们解决问题的方法有很多种，其中最常见的当属牛顿力学。但是在实际问题中，有时候使用拉格朗日力学会比牛顿力学更加方便。那么，什么情况下使用拉格朗日力学会更加方便呢？

本文将通过弹簧摆和双摆两个案例来说明拉格朗日力学在实际应用中的优越之处。拉格朗日力学是一种描述物体运动的方法。它需要时间t，广义坐标q以及广义坐标对时间的导数（广义速度）来描述物体的运动状态。

在机械运动情况下，考虑不含时的系统，它的拉氏量就有如下形式：这里，拉氏量是广义坐标与它们对时间的导数的函数。在现实中，物体总是沿着某一条路径运动。当在地球上低速情况下，决定粒子路径的规律正是牛顿力学。

不妨假设物体运动在一维空间中，在t1时刻的广义坐标为q1，t2时刻为q2，并且对于这两个路径的端点，广义速度也是确定的。那么，什么情况下使用拉格朗日力学会更加方便呢？下面我们通过弹簧摆和双摆两个案例来说明。首先，我们来看弹簧摆的情况。

弹簧摆的拉氏量可以表示为：其中，m是弹簧质量，k是弹性系数，l是弹簧原长，g是重力加速度。通过对这个拉氏量进行变分，我们可以得到弹簧摆的运动方程。接着，我们来看双摆的情况。双摆有两个自由度，可以用两个广义坐标来描述。对于单摆，我们可以通过牛顿第二定律来求解。

但是对于双摆，使用牛顿第二定律会很麻烦，而使用拉格朗日力学则会更加方便。双摆的拉氏量可以表示为：其中，m1和m2分别是两个质点的质量，l1和l2分别是两个摆线的长度，g是重力加速度，θ1和θ2分别是两个质点的角度。

通过对这个拉氏量进行变分，我们可以得到双摆的运动方程。可以发现，使用拉格朗日力学求解双摆的运动方程远比使用牛顿第二定律方便。综上所述，当我们遇到多自由度的问题时，使用拉格朗日力学会更加方便。此外，在某些特殊情况下，使用拉格朗日力学也会比使用牛顿力学更加方便。

总之，拉格朗日力学在物理学中有着广泛的应用，它不仅仅是一种物理学方法，还是一种物理哲学。因此，我们应该在学习物理学的过程中，尽可能地掌握拉格朗日力学的知识。你认为，在实际问题中，何时使用拉格朗日力学会更加方便？请留言讨论。

本文主要讲述了拉格朗日力学的变分原理和应用。拉格朗日力学是一种可以用于描述运动物体的力学系统的工具，其基本思想是建立一个由动能和势能组成的拉氏量，然后通过对拉氏量进行变分来推导出物体的运动方程。本文通过弹簧摆和双摆两个例子来阐述拉格朗日力学的应用。

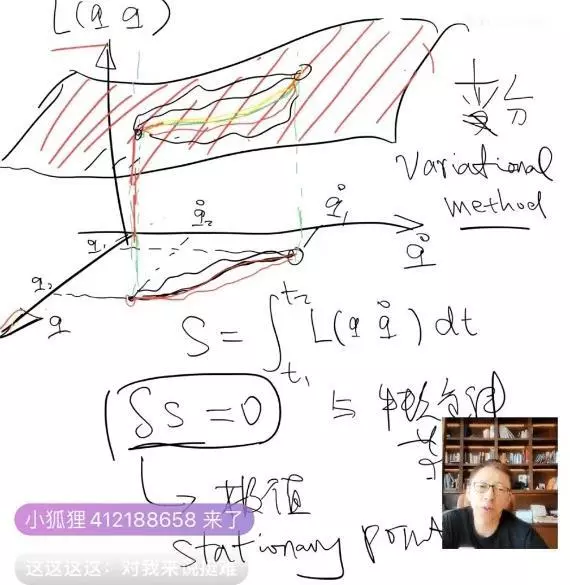
首先，本文介绍了拉格朗日力学的变分原理，即作用量在变分的操作下取极值的原理。拉格朗日力学的核心在于建立一个由动能和势能组成的拉氏量，然后通过对拉氏量进行变分来推导出物体的运动方程。本文中还给出了相应的拉氏量满足的微分方程，即Euler-Lagrange方程。

接下来，本文通过弹簧摆这个例子来阐述拉格朗日力学的应用。弹簧摆是一个弹簧下悬挂一个小球的系统，小球会沿着弹簧方向振动的同时随弹簧一起摆动。本文首先使用牛顿力学对这一系统进行受力分析，然后通过拉格朗日力学的方法来研究弹簧摆的运动方程。

可以看到，通过拉格朗日力学得到的运动方程和用牛顿力学得到的方程完全一致。但由于径向的运动和角向的运动是耦合的，方程无法解析求解，因此本文展示了数值计算得到的图象化结果，可以看到出现了混沌现象，这一系统是对初值敏感的。最后，本文介绍了双摆这个例子。

双摆由两个小球组成，摆动的角度分别为theta1和theta2。使用牛顿力学分析比较困难，但是使用拉格朗日力学会相对容易许多。本文通过建立系统的动能和势能来构建拉氏量，并通过对拉氏量进行变分来推导出双摆的运动方程。

综上所述，拉格朗日力学是一种可以用于描述运动物体的力学系统的工具。本文通过弹簧摆和双摆两个例子来阐述了拉格朗日力学的应用，展示了其在物理学中的重要性和广泛应用价值。最后，提出一个问题，读者们在日常生活中是否还能找到其他应用拉格朗日力学的例子？

双摆运动的拉格朗日量分析双摆是一个简单而又经典的力学问题，它的运动规律可以用拉格朗日力学来描述。在《张朝阳的物理课》中，张朝阳深入浅出地解析了双摆的拉格朗日量，并用欧拉-拉格朗日方程得到了双摆的运动方程。首先，我们需要了解双摆的基本结构。

双摆由两个摆锤和一个铰链连接而成，第一个摆锤的摆长为l1，第二个摆锤的摆长为l2，两个摆锤的质量分别为m1和m2。考虑到双摆的运动是二维的，我们需要将摆锤的运动分解为竖直和水平两个方向。因此，每个摆锤的运动状态可以用两个广义坐标θ1和θ2来描述。

接下来，我们需要推导双摆的拉格朗日量。由于摆锤在运动中同时受到重力和张力的作用，我们需要分别计算它们的势能和动能。

对于每个摆锤，它的动能可由其速度平方的一半表示，即T1=(1/2)m1(l1^2)(θ1')^2和T2=(1/2)m2[(l1^2)(θ1')^2+(l2^2)(θ2')^2+2l1l2θ1'θ2'cos(θ1-θ2)]。

摆锤的势能则可以看作是其离开平衡位置所带来的重力势能，即V1=m1gl1(1-cosθ1)和V2=m2g(l1(1-cosθ1)+l2(1-cosθ2))。将上述动能和势能相加，我们就可以得到双摆的拉格朗日量L=T1+T2-V1-V2。

接下来，我们可以使用欧拉-拉格朗日方程求解双摆的运动方程。通过对欧拉-拉格朗日方程进行求解，我们可以得到双摆的加速度随时间变化的方程式。这个方程式可以帮助我们预测双摆在不同条件下的运动状态，进而深入探究双摆运动的规律。

总之，双摆的运动规律可以用拉格朗日力学来描述，张朝阳通过对双摆的拉格朗日量进行分析，得到了双摆的运动方程。这个问题的解决不仅有利于我们更深入地了解物理学中的拉格朗日力学，同时也具有一定的实际应用价值。