5个拉格朗日点分别在哪

宇宙的万有引力现象，在天体间反应得特别清楚，几乎任何相近的天体间都能看出引力的作用，特别是像太阳系这样稳定运行的恒星行星系统，引力的作用显而易见。

在两个天体间的不同位置，引力的作用也是不同的，这种现象在拉格朗日点上反映的特别清楚，拉格朗日点是指在两大物体引力作用下，能使小物体处于特殊状态的点，于1772年由法国数学家拉格朗日推算得出，如今已在宇航学中广泛应用。

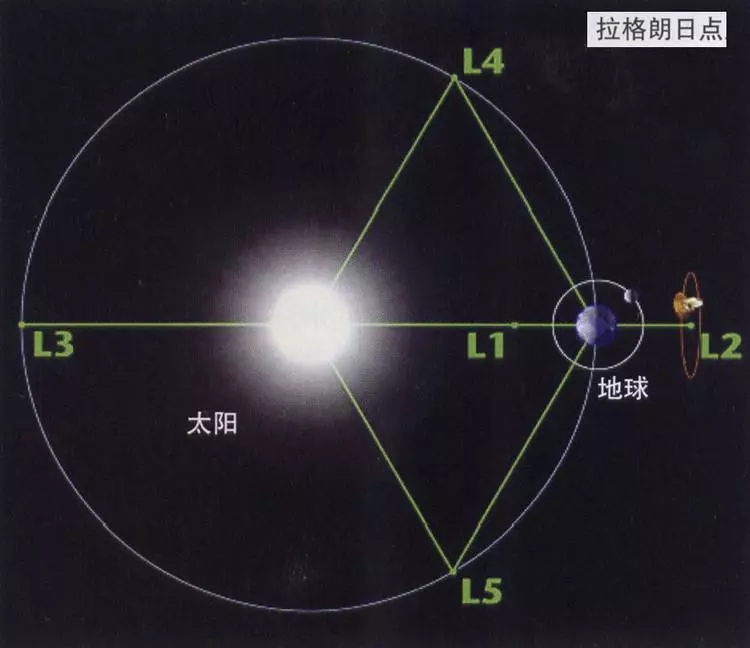
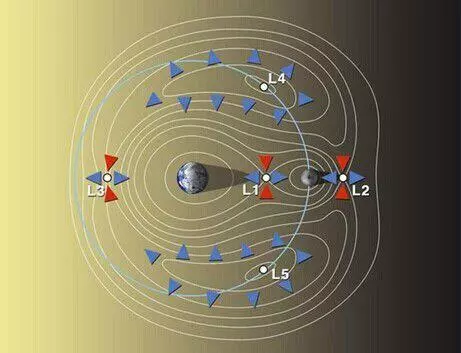
拉格朗日发现这种奇异点在天体运动系统中有5个，用字母L表示。L1、L2和L3在两个天体的联线上，为不稳定点。如一个物体在这些点上稍微挪动一下，就会离去，不再复位。L4、L5则是稳定点，不容易离去。

反映到宇宙天体上，任何相互间有引力的两个天体都有五个拉格朗日点，它存在于双星系统、行星和太阳、卫星和行星 的轨道面上。都是其中的L4、L5两个点稳定，另三个L1、L2和L3的拉格朗日点不很稳定，但是都有其利用价值。

在地球和太阳的轨道和地球与月亮的轨道上，当然也有这样的点。那么这些点有什么好处呢！其实在宇航领域好处很多，首先在这个地方可以节省航天器的燃料，保持航天器的稳定姿态，使航天器易于跟踪、操作和维护等等，因此这些拉格朗日点今后必将成为航天大国发射航天器时的必争之地。

以地球和太阳为例，如果一个物体在地球与太阳之间，地球引力的影响会减弱太阳对这物体的拉力，物体距地球越近，这种影响就越大，因此增加了这个物体的轨道周期。在L1点，物体的轨道周期则恰好等于地球的轨道周期，利用日地拉格朗日点L1的这种特性，美国宇航局和欧洲空间局共同发射的太阳及日光层探测仪就围绕日地系统的L1点运行。

拉格朗日点L2则在两个大天体的连线上，且在较小的天体一侧。当一个物体距太阳的距离越远，它的轨道周期通常就越长。但地球引力对其的拉力又减小了物体的轨道周期。所以在在L2点，它的轨道周期又变得与地球相等了。所以这个位置 通常用于放置空间天文台，因为L2的物体可以保持背向太阳和地球的方位，易于保护和校准。威尔金森微波各向异性探测器（美国）和詹姆斯·韦伯太空望远镜（美国）就是被放置在日-地系统的L2点上运行。L3、L4、L5也是各有用处，今后，在这些点上的航天器将会越来越多。

从上面的介绍中也可以看出，在这方面美国已经先行一步，其实不单是在日地拉格朗日点上，在地月拉格朗日点上同样如此，美国宇航局早就计划在地月拉格朗日点L2上建设月球空间站，处于地月拉格朗日点上的空间站能够为宇航员和工程师积累深空操作的经验，最终会确保人类脱离地月系统而探索更为广阔的宇宙空间，同时还能够作为维修大型天文望远镜的平台，并且由于地月拉格朗日点距离月球较近，因此还可以用来对月球上的地质勘探机器人进行实时遥控。

世界各大国都非常重视玉衡事业的发展，今后中国、俄罗斯、欧洲、印度、日本、巴西，加拿大、澳大利亚等国和地区都将在太空领域展开竞争，但是地球和太阳以及地球和月亮之间却只有那么几个拉格朗日点，因此这些虚无的地点今后将必成航天大国的必争之地，而当人类的航天器在这里越来越集中的时候，互相干扰和相撞的可能性就增加了，就像移动中的车辆撞到静止中的车辆需要担责一样，谁先来到这里占据有利地点，将不但有利于科学研究，更因之具备了道义和公理上的优越性，这就是太空中的“自古以来”，通常，“自古以来”的地方都是能者居之，所以也希望我们能在太空中多拥有几个“自古以来”。